Page 41 - 理化检验-物理分册2024年第六期

钱海玥，等：典型悬挂物结构特征参数分布特性及回归分析

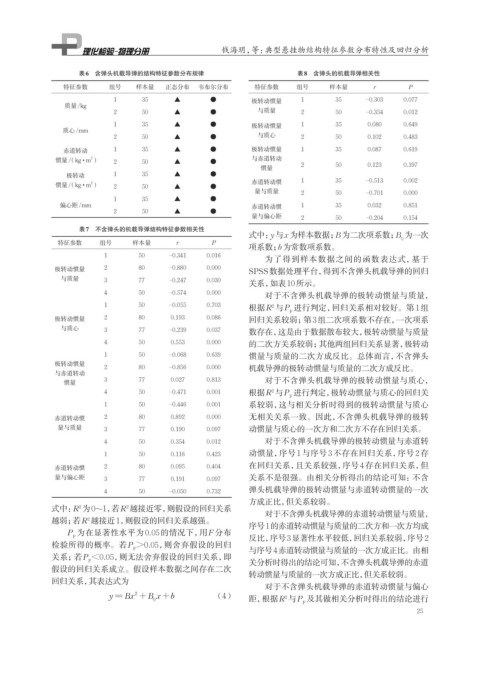
表6 含弹头机载导弹的结构特征参数分布规律 表8 含弹头的机载导弹相关性
特征参数 组号 样本量 正态分布 韦布尔分布 特征参数 组号 样本量 r P

1 35 ▲ ● 极转动惯量 1 35 ‒0.303 0.077
质量/kg
2 50 ▲ ● 与质量 2 50 ‒0.354 0.012
1 35 ▲ ● 极转动惯量 1 35 0.080 0.649
质心/mm
2 50 ▲ ● 与质心 2 50 0.102 0.483
赤道转动 1 35 ▲ ● 极转动惯量 1 35 0.087 0.619
2
惯量/（kg·m ） 2 50 ▲ ● 与赤道转动
惯量 2 50 0.123 0.397
极转动 1 35 ▲ ●
赤道转动惯 1 35 ‒0.513 0.002
2
惯量/（kg·m ） 2 50 ▲ ●
量与质量 2 50 ‒0.701 0.000
1 35 ▲ ●
偏心距/mm 赤道转动惯 1 35 0.032 0.851
2 50 ▲ ●
量与偏心距 2 50 ‒0.204 0.154
表7 不含弹头的机载导弹结构特征参数相关性
式中：y与x为样本数据；B为二次项系数；B 为一次
特征参数 组号 样本量 r P 0
项系数；b为常数项系数。
1 50 ‒0.341 0.016
为了得到样本数据之间的函数表达式，基于
极转动惯量 2 80 ‒0.880 0.000 SPSS数据处理平台，得到不含弹头机载导弹的回归
与质量 3 77 ‒0.247 0.030
关系，如表10所示。
4 50 ‒0.574 0.000
对于不含弹头机载导弹的极转动惯量与质量，
1 50 ‒0.055 0.703 根据R 与P 进行判定，回归关系相对较好。第1组
2
F
极转动惯量 2 80 0.193 0.086 回归关系较弱；第3组二次项系数不存在，一次项系
与质心 3 77 ‒0.239 0.037 数存在，这是由于数据散布较大，极转动惯量与质量
4 50 0.553 0.000 的二次方关系较弱；其他两组回归关系显著，极转动
1 50 ‒0.068 0.639 惯量与质量的二次方成反比。总体而言，不含弹头
极转动惯量
2 80 ‒0.856 0.000 机载导弹的极转动惯量与质量的二次方成反比。
与赤道转动
惯量 3 77 0.027 0.813 对于不含弹头机载导弹的极转动惯量与质心，
2
4 50 ‒0.471 0.001 根据R 与P 进行判定，极转动惯量与质心的回归关
F
1 50 ‒0.446 0.001 系较弱，这与相关分析时得到的极转动惯量与质心
赤道转动惯 2 80 0.892 0.000 无相关关系一致。因此，不含弹头机载导弹的极转
量与质量 3 77 0.190 0.097 动惯量与质心的一次方和二次方不存在回归关系。
4 50 0.354 0.012 对于不含弹头机载导弹的极转动惯量与赤道转
1 50 0.116 0.423 动惯量，序号1与序号3不存在回归关系，序号2存
赤道转动惯 2 80 0.095 0.404 在回归关系，且关系较强，序号4存在回归关系，但
量与偏心距 3 77 0.191 0.097 关系不是很强。由相关分析得出的结论可知：不含
弹头机载导弹的极转动惯量与赤道转动惯量的一次
4 50 ‒0.050 0.732
方成正比，但关系较弱。
式中：R 为0~1，若R 越接近零，则假设的回归关系
2
2
对于不含弹头机载导弹的赤道转动惯量与质量，
越弱；若R 越接近1，则假设的回归关系越强。
2
序号1的赤道转动惯量与质量的二次方和一次方均成
P 为在显著性水平为0.05的情况下，用F分布
F 反比，序号3显著性水平较低，回归关系较弱，序号2
检验所得的概率。若P >0.05，则舍弃假设的回归
F 与序号4赤道转动惯量与质量的一次方成正比。由相
关系；若P <0.05，则无法舍弃假设的回归关系，即
F 关分析时得出的结论可知，不含弹头机载导弹的赤道
假设的回归关系成立。假设样本数据之间存在二次
转动惯量与质量的一次方成正比，但关系较弱。
回归关系，其表达式为
对于不含弹头机载导弹的赤道转动惯量与偏心
y = 2 +Bx +B x b （4）
2
0 距，根据R 与P 及其做相关分析时得出的结论进行
F
25