Page 28 - 理化检验-物理分册2024年第五期

赵如涛, 等: 塑性变形对低合金钢拉伸性能的影响

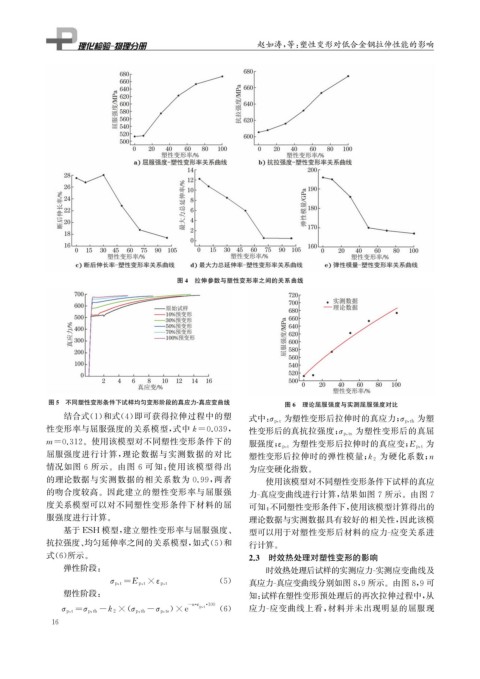
图4 拉伸参数与塑性变形率之间的关系曲线

图5 不同塑性变形条件下试样均匀变形阶段的真应力 - 真应变曲线 图6 理论屈服强度与实测屈服强度对比
结合式( 1 ) 和式( 4 ) 即可获得拉伸过程中的塑 为塑
式中: σ p , t 为塑性变形后拉伸时的真应力; σ p , tb
性变形率与屈服强度的关系模型, 式中k=0.039 , 为塑性变形后的真屈
性变形后的真抗拉强度; σ p , ts
m=0.312 。使用该模型对不同塑性变形条件下的 为
服强度; ε p , t 为塑性变形后拉伸时的真应变; E p , t
屈服强度进行计算, 理论数据与实测数据的对比
塑性变形后拉伸时的弹性模量; k 2 为硬化系数; n
情况如图 6 所示。由图 6 可知: 使用该模型得出 为应变硬化指数。
的理论数据与实测数据的相关系数为 0.99 , 两者 使用该模型对不同塑性变形条件下试样的真应
的吻合度较高。因此建立的塑性变形率与屈服强
力 - 真应变曲线进行计算, 结果如图7所示。由图7
度关系模型可以对不同塑性变形条件下材料的屈 可知: 不同塑性变形条件下, 使用该模型计算得出的
服强度进行计算。 理论数据与实测数据具有较好的相关性, 因此该模
基于 ESH 模型, 建立塑性变形率与屈服强度、 型可以用于对塑性变形后材料的应力 - 应变关系进
抗拉强度、 均匀延伸率之间的关系模型, 如式( 5 ) 和 行计算。
式( 6 ) 所示。 2.3 时效热处理对塑性变形的影响
弹性阶段: 时效热处理后试样的实测应力 - 实测应变曲线及
( 5 ) 真应力 - 真应变曲线分别如图8 , 9所示。由图8 , 9可
σ p , t= E p , t× ε p , t
塑性阶段: 知: 试样在塑性变形预处理后的再次拉伸过程中, 从
- n · ε , 100 应力 - 应变曲线上看, 材料并未出现明显的屈服现
·
(
)
σ p , t= σ p , tb- k 2× σ p , tb- σ p , ts ×e pt ( 6 )
1 6