Page 44 - 理化检验-物理分册2022年第十期

叶盛春, 等: 不等厚 P92 钢弯头的球形缺陷应力分析及预测

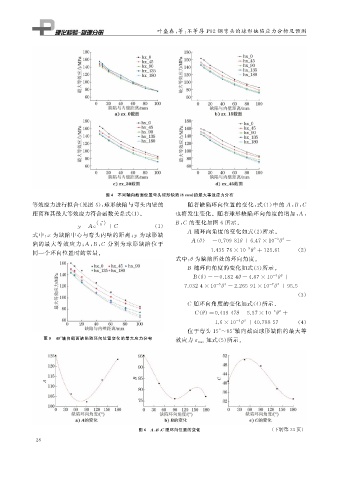
图4 不同轴向截面位置弯头球形缺陷( 8mm ) 的最大等效应力分布
等效应力进行拟合( 见图 5 ), 球形缺陷与弯头内壁的 随着缺陷环向位置的变化, 式( 1 ) 中的 A , B , C
距离和其最大等效应力符合函数关系式( 1 )。 也将发生变化。随着球形缺陷环向角度的增加, A ,
- x
B B , C 的变化如图 6 所示。
y=Ae +C ( 1 )
式中: x 为缺陷中心与弯头内壁的距离; 为球形缺 A 随环向角度的变化如式( 2 ) 所示。
y

- 3 2
陷的最大等效应力; A , B , C 分别为球形缺陷位于 A ( θ ) =- 0.70981 θ+6.47×10 θ -

- 5 3 ( 2 )
同一个环向位置时的常量。 1.43576×10 θ +125.61
式中: θ 为缺陷所处的环向角度。
B 随环向角度的变化如式( 3 ) 所示。

B ( θ ) =- 0.1824θ-4.87×10 θ +
- 3 2

- 5 3 - 7 4
7.0324×10 θ -2.26591×10 θ +95.5
( 3 )
C 随环向角度的变化如式( 4 ) 所示。

- 3 2
=
C ( θ ) 0.43947θ-5.57×10 θ +

- 5 3 ( 4 )
1.6×10 θ +40.78857
位于弯头 15°~85° 轴向截面球形缺陷的最大等
图 5 45° 轴向截面缺陷随环向位置变化的最大应力分布 如式( 5 ) 所示。
效应力σ max

图6 A , B , C 随环向位置的变化 ( 下转第33页)
2 8