Page 26 - 理化检验-物理分册2022年第二期
P. 26
凃应宏, 等: ISO10113 : 2020 标准中若干技术问题的验证
与理想值存在 靠近内侧, 曲线收敛得越早, 收敛程度越理想。
以看出, 只要纵向引伸计的标距 L e
偏离, 那么r 值的波动将不可避免。在实际测试过 ( 2 )应变水平越小, 弹性扣除对r 值造成的理
程中, 肯定还叠加有其他的影响因素, r 值的波动性 论影响就越大。以 BUSD-A 试样为例, 一个r 值为
有可能缓解也可能进一步加剧。 2.6 的理想试样在应变为 5% 时: 如果材料的屈服强
表 4 测试系统逻辑性错位对r 值的影响 度等级为200MPa , 则r 值将偏高0.10 ; 如果屈服强
引伸计 约定 实际 纵向引伸计 横向引伸计 度提高到600MPa , 则r 值将偏高0.35 ; 随着应变水
编号 应变 / % 应变 / % 认定 ΔL / mm 测得 Δb / mm r 15
平的增加, 这种影响将逐步减弱, 在应变为 15% 时,
B 15.0 14.85 7.500 1.190 2.52
两者间的理论差异可减小到小于 0.05 ( 见图 15 )。
C 15.0 14.93 7.500 1.195 2.56
D 15.0 15.00 7.500 1.200 2.60
E 15.0 15.08 7.500 1.206 2.65
F 15.0 15.15 7.500 1.211 2.69
r 值的准确性完全取决于试样的纵向变形和横
向变形能否被准确地测试出来, 并且在测试的同时,
不扭曲两者之间( 几何上以及逻辑上) 的对应关系,
目前广泛采用的全自动引伸计可能存在着如下几个
问题。
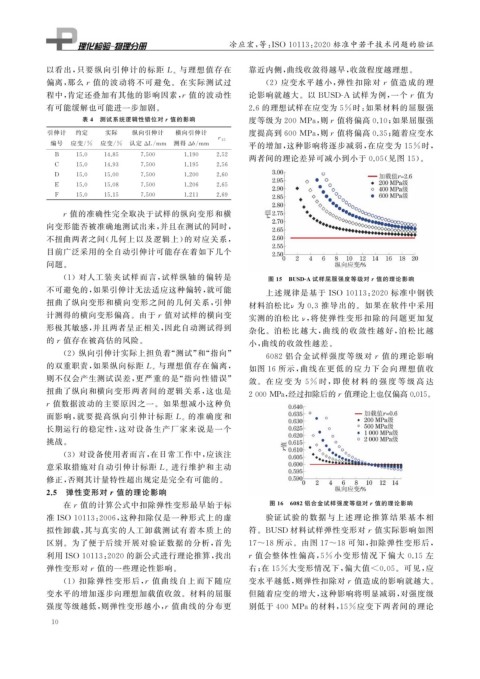
( 1 )对人工装夹试样而言, 试样纵轴的偏转是 图 15 BUSD-A 试样屈服强度等级对r 值的理论影响
不可避免的, 如果引伸计无法适应这种偏转, 就可能 上述规律是基于ISO10113 : 2020 标准中钢铁
扭曲了纵向变形和横向变形之间的几何关系, 引伸 材料泊松比 ν 为 0.3 推导出的。如果在软件中采用
计测得的横向变形偏高。由于r 值对试样的横向变 实测的泊松比ν , 将使弹性变形扣除的问题更加复
形极其敏感, 并且两者呈正相关, 因此自动测试得到 杂化。泊松比越大, 曲线的收敛性越好, 泊松比越
的r 值存在被高估的风险。
小, 曲线的收敛性越差。
( 2 )纵向引伸计实际上担负着“ 测试” 和“ 指向” 6082 铝合金试样强度等级对r 值的理论影响
与理想值存在偏离,
的双重职责, 如果纵向标距 L e 如图 16 所示, 曲线在更低的应力下会向理想值收
则不仅会产生测试误差, 更严重的是“ 指向性错误” 敛。在 应 变 为 5% 时, 即 使 材 料 的 强 度 等 级 高 达
扭曲了纵向和横向变形两者间的逻辑关系, 这也是
2000MPa , 经过扣除后的r 值理论上也仅偏高0.15 。
0
r 值数据波动的主要原因之一。如果想减小这种负
的准确度和
面影响, 就要提高纵向引伸计标距 L e
长期运行的稳定性, 这对设备生产厂家来说是一个
挑战。
( 3 )对设备使用者而言, 在日常工作中, 应该注
进行维护和主动
意采取措施对自动引伸计标距 L e
修正, 否则其计量特性超出规定是完全有可能的。
2.5 弹性变形对r 值的理论影响
在r 值的计算公式中扣除弹性变形最早始于标 图 16 6082 铝合金试样强度等级对r 值的理论影响
准ISO10113 : 2006 , 这种扣除仅是一种形式上的虚 验证试验的数据与上述理论推算结果基本相
拟性卸载, 其与真实的人工卸载测试有着本质上的 符。 BUSD 材料试样弹性变形对r 值实际影响如图
区别。为了便于后续开展对验证数据的分析, 首先 17~18 所示。由图 17~18 可知, 扣除弹性变形后,
利用ISO10113 : 2020 的新公式进行理论推算, 找出 r 值会整体性偏高, 5% 小变形情况下偏大 0.15 左
弹性变形对r 值的一些理论性影响。 右; 在 15% 大变形情况下, 偏大值 <0.05 。可见, 应
( 1 )扣除弹性变形后, r 值曲线自上而下随应 变水平越低, 则弹性扣除对r 值造成的影响就越大。
变水平的增加逐步向理想加载值收敛。材料的屈服 但随着应变的增大, 这种影响将明显减弱, 对强度级
强度等级越低, 则弹性变形越小, r 值曲线的分布更 别低于 400MPa的材料, 15% 应变下两者间的理论
1 0