Page 21 - 理化检验-物理分册2018第四期

白 涛, 等: 三类内应力之间的关系及其对疲劳的作用

错组态, 与图 １２a ) 中的理想晶粒有很大的区别.
分析变形金属时, 由于物理模型与实际结构的
差距如此之大, 因此华丽的数学处理只能如同建在
沙漠上的高楼, 只有在无位错的陶瓷粒度分析上, 谱
型分析才能取得较好的效果.

２ 三类内应力对疲劳的作用

２．１ I类应力对疲劳的作用
国内有文献认为I类应力即宏观应力或残余应
力, 可以和外载应力取代数和, 即压应力直接抵消疲
劳应力.但残余应力是静应力, 而疲劳应力为动应
力, 两者之间的关系如图 １３ 中平均应力和交变应力
的关系.残余应力可以看成为平均应力, 疲劳应力
是交变应力.静、 动 应 力 间 应 该 用 Goodman 关 系
表述, 如图 １４ 所示, 用数学公式表达如下
－ １ － １ ( １ )
σ m ＝ σ －mσ m
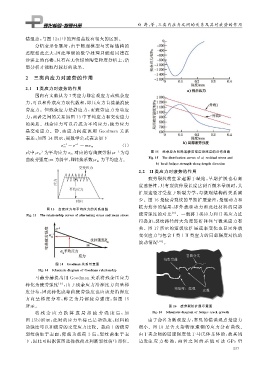
式中: σ m 为平均应力σ m 对应的弯曲疲劳限; σ 为弯 图 １５ 残余应力和局部疲劳强度沿深度的分布曲线
－１
－１
Fi g 敭１５ Thedistributioncurvesofa residualstressand
曲疲劳强度; m 为斜率, 即转换系数; σ m 为平均应力.
b localfati g uestren g thalon gdee p thdirection
２．２ II类应力对疲劳的作用
疲劳裂纹萌生常起源于缺陷, 早期扩展也有高
度选择性, 只有裂纹伸展长度达到百微米量级时, 其
扩展途径才受控于断裂力学, 与微观结构的关系减
少.图 １６ 是疲劳裂纹的早期扩展途径, 是驱动力和
抗力博弈的结果, 即外载驱动力和此处材料的局部
图 １３ 交变应力与平均应力的关系曲线
疲劳强度的对比 [ ９ ] .一般将I类应力和II类应力进
Fi g 敭１３ Therelationshi p curvesofalternatin g stressandmeanstress
行叠加, 裂纹路径的大角度转折往往与微观应力有
关.图 １７ 所示的短裂纹扩展速率变化也显示外载
交变应力与包含I类 ＋II类应力的局部强度对抗的
波动情况 [ １０ ] .

图 １４ Goodman关系示意图
Fi g 敭１４ Schematicdia g ramofGoodmanrelationshi p
马赫劳赫提出用 Goodman 关系将残余压应力
转化为疲劳强度 [ ８ ] , 由于残余应力沿深度方向呈梯
度分布, 因此转化成弯曲疲劳强度也应该是沿深度

方向 呈 梯 度 分 布, 称 之 为 局 部 疲 劳 强 度, 如 图 １５
所示. 图 １６ 疲劳裂纹扩展示意图
将 残 余 应 力 换 算 成 局 部 疲 劳 强 度 后,如 Fi g 敭１６ Schematicdia g ramoffati g uecrackg rowth
图 １５b ) 所示, 此时的应力坐标已是动强度, 材料的 由于命名为微观应力, 常见的错误观点是应力
动强度可以和疲劳的交变应力比较.载荷 １ 的疲劳 很小.图 １８ 是含夹杂物滚珠钢的应力分布曲线.
裂纹萌生于表面, 降载为载荷 ２ 后, 裂纹萌 生于表 由于夹杂物的屈服强度低于马氏体基体的, 故其周
下, 因此可根据该图选择载荷及判断裂纹萌生部位. 边发生 应 力 松 弛, 两 者 之 间 的 差 值 可 达 GPa 量
２ ３ ７