Page 18 - 理化检验-物理分册2018第四期

白 涛, 等: 三类内应力之间的关系及其对疲劳的作用

方面也发现多相材料不同晶粒间的应力也可以引起
谱线位移, 与定义不符.
德国科学家马赫劳赫对内应力重新定义如下: 第
I类应力σ I 在材料的宏观范围内平衡, 当平衡破坏时
有尺寸变化; 第II类应力σ II 在晶粒尺度内平衡, 当平
衡破坏时有尺寸变化; 第III类应力σ III 存在于原子尺
图 ３ 三类内应力分布曲线关系
度, 平衡破坏时不会发生尺寸变化 [ ２ ] .三类内应力之
Fi g 敭３ Thedistributioncurverelationshi p ofthreet yp esofinternalstresses
间的关系如图１ ( 图中x , 表示空间位置) 所示.
y

图 ４ I类和II类应力合成示意图
Fi g 敭４ Schematicdia g ramofcom p ositionof σ Iandσ II
达维金科夫定义三类内应力的依据是 X 射线
衍射效应, 但未说明三类内应力之间的关系.马赫
劳赫描述了材料中三类内应力之间的关系, 但无衍
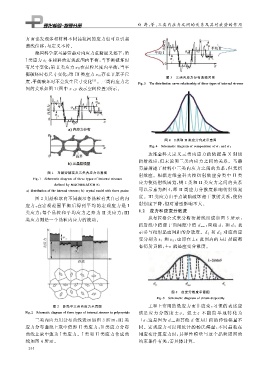
图 １ 马赫劳赫定义三类内应力示意图
射效应.根据达维金科夫按衍射效应分类中 II类
Fi g 敭１ Schematicdia g ramofthreet yp esofinternalstresses
应力使衍射线展宽, 则I类和II类应力之间的关系
definedb yMACHERAUCHE
可以示意为图 ４ , 即 II类应力分散度影响衍射线宽
a distributionoftheinternalstresses b cr y stalmodelwiththree g rains
图 ２ 用晶粒取向不同表示各晶粒有其自己的内 度. III类应力由于点缺陷破坏相干散射关系, 使衍
射强度下降, 但对谱型影响不大.
应力, 在宏观范围平衡后得到平均的宏观应力是 I
１．２ 应力和应变分散度
类应力; 每个晶粒和平均应力之差为 II类应力; III
从布拉格公式来分析衍射线组成如图 ５ 所示,
类应力则是一个晶粒内应力的波动.
衍射线中值源于面间距中值 d ave 两端 d １ 和 d ２ 表
,
示参与衍射晶面间距的分散度. d １ 和d ２ 对应的应
变分别为ε １ 和ε ２ 也即在 ± ε 范围内的hkl 晶面都
,
有衍射贡献, ± ε 就是应变分散度.

图 ５ 应变分散度示意图
Fi g 敭５ Schematicdia g ramofstraindis p ersit y
图 ２ 多晶中三类内应力示意图 工程上常用的是应力而非应变, 习惯的表述应
Fi g 敭２ Schematicdia g ramofthreet yp esofinternalstressesinp ol y cr y stals 该是 应 力 分 散 度 ±σ .但 ±ε 不 能 简 单 地 转 化 为
三类内应力用分布曲线表示如图 ３ 所示, III类 ±σ , 这是因为d ave 和其他d 值hkl 面的弹性模量不
应力分布曲线上取中值即II类应力, II类应力分布 同.宏观应力可以用统计的杨氏模量, 不同晶粒在
曲线上取中值为I类应力. I类和II类应力合成曲 用应变计算应力时, 其弹性模量与这个晶粒周围的
线如图 ４ 所示. 约束条件有关, 需具体计算.
２ ３ ４