Page 20 - 理化检验-物理分册2024年第三期

高宇昊, 等: 柔度法测算三点弯曲试样疲劳裂纹长度的影响因素

/
/

a s W ≤0.2 时, a( 3 ) / W 与a s W 差值比a( 1 ) / W 与 当试样厚度不大于 40mm 时, 在平直贯穿型裂
a s W 差值明显偏小; 当 a s W ≥0.3 时, a( 3 ) / W 与 纹情况下, 裂纹中心的平面应变状态对柔度函数关
/
/
a s W 差值小于 2% ; 当a s W ≥0.3 时, 柔度函数关 系没有明显的影响, 当a s W ≥0.3 时, 在式( 1 ) 中使
/
/
/
系式与有限元模拟结果较为符合, 侧面验证了柔度 用材料的弹性模量 E 进行计算, 可以获得较准确的
函数关系的正确性。 测算裂纹长度。

图 6 两柔度公式测算裂纹长度与模拟裂纹长度的关系
3.3 裂纹曲率对柔度法测算裂纹长度的影响 明显; 随着试样厚度的增大, 圆弧角度2α 增大, 且具
在金属材料的疲劳裂纹扩展速率试验中, 裂纹 有明显的增长趋势。圆弧角度 2 α 不但与曲率半径
中心处的材料处于平面应变状态, 承受的应力比试 R 有关, 还有试样厚度有关, 因此对于不同厚度的试
样两侧的应力大, 因此中心处的裂纹扩展速率较快, 样, 圆弧角度 2 α 比曲率半径 R 更能近似地描述裂
两侧的裂纹扩展速率较慢, 裂纹 前缘类似圆弧状。 纹前缘的弯曲程度。
用圆弧近 似 裂 纹 前 缘 的 形 状, 根 据 最 大 裂 纹 长 度
与试样厚度 B 之间的几何
a max 、 最小裂纹长度a min
关系, 裂纹前缘的弯曲半径 R , 圆弧角度 2α 的计算
关系分别如式( 5 ) ~ ( 7 ) 所示。
B 2
(
2
2
R = 2 + R -d ) ( 5 )
( 6 )
d = a max - a min
B
sin α= 2 / R ( 7 )
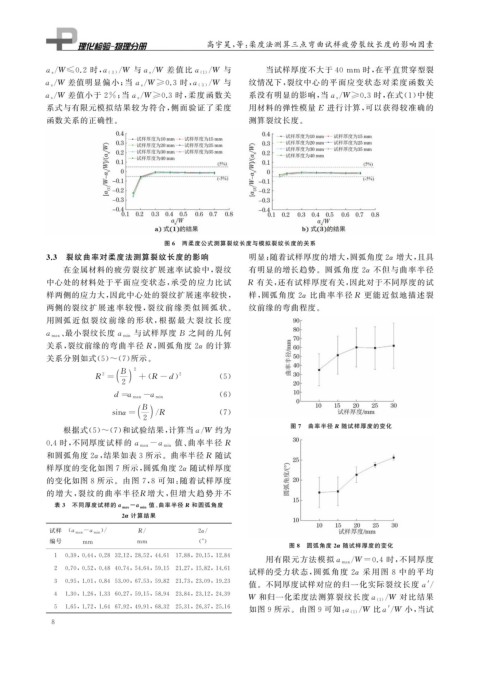
图 7 曲率半径 R 随试样厚度的变化
根据式( 5 ) ~ ( 7 ) 和试验结果, 计算当a / W 约为
值、 曲率半径 R
0.4 时, 不同厚度试样的 a max-a min
和圆弧角度2 α , 结果如表3 所示。曲率半径 R 随试
样厚度的变化如图7 所示, 圆弧角度2 α 随试样厚度
的变化如图 8 所示。由图 7 , 8 可知: 随着试样厚度
的 增大, 裂纹的曲率半径 R 增大, 但增大趋势并不
值、 曲率半径 R 和圆弧角度
表 3 不同厚度试样的a max -a min
2α 计算结果
试样 ( a max - a min )/ R / 2α /
编号 mm mm ( ° )
图 8 圆弧角度 2α 随试样厚度的变化

1 0.39 , 0.44 , 0.28 32.12 , 28.52 , 44.61 17.88 , 20.15 , 12.84
用有限元方法模拟a max W =0.4 时, 不同厚度
/

2 0.70 , 0.52 , 0.48 40.74 , 54.64 , 59.15 21.27 , 15.82 , 14.61
试样的受力状态, 圆弧角度 2 α 采用图 8 中的平均

3 0.95 , 1.01 , 0.84 53.00 , 67.53 , 59.82 21.73 , 23.09 , 19.23
值。不同厚度试样对应的归一化实际裂纹长度a' /

W 和归一化柔度法测算裂纹长度a( 1 ) / W 对比结果
4 1.30 , 1.26 , 1.33 60.27 , 59.15 , 58.94 23.84 , 23.12 , 24.39

5 1.65 , 1.72 , 1.64 67.92 , 49.91 , 68.32 25.31 , 26.37 , 25.16 如图9 所示。由图9 可知: a( 1 ) / W 比 a' / W 小, 当试
8