Page 40 - 理化检验-物理分册2022年第十二期

王程明, 等: 工程机械用 Q690 钢的热变形行为

当变形温度和应变速率一定时, 将式( 2 ) 两边分
̇ n RT ( 1 )
Q d
ε=A sinhασ p ex p -
̇
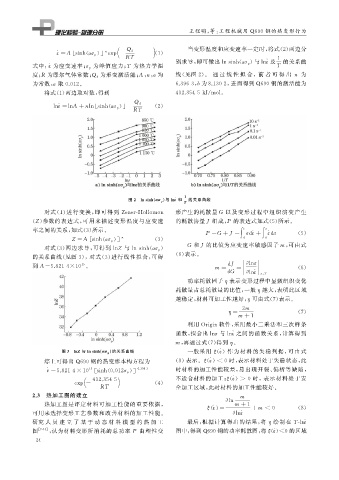
) 与 lnε 及 1 的关系曲

别求导, 即可做出lnsinh ( ασ p
ε 为峰值应力; T 为热力学温 T
式中: ̇ 为应变速率; σ p
为形变激活能; A , n , α 均 线( 见图 2 )。 通 过 线 性 拟 合,前 者 可 得 出 n 为
度; R 为摩尔气体常数; Q d

为常数, α 取 0.012 。 6.3963 , b 为8.1302 , 进而得到 Q690 钢的激活能为

将式( 1 ) 两边取对数, 得到 432.3545kJ / mol 。
̇
lnε= lnA +nln sinhασ p - Q d ( 2 )

RT

1

̇
) 与ln ε 和 的关系曲线
图 2 lnsinh ( ασ p
T
对式( 1 ) 进行变换, 即可得到 Zener-Hollomon 形产生的耗散量 G 以及变形过程中组织演变产生
( Z ) 参数的表达式, 可用来描述变形温度与应变速 的耗散协量J 组成, P 的表达式如式( 5 ) 所示。
̇ ε σ
率之间的关系, 如式( 3 ) 所示。 ̇ ̇
P =G +J = σd ε+ ε dσ ( 5 )
n ∫ ∫
0
0

Z =A sinhασ p ( 3 )

G 和J 的比值为应变速率敏感因子 m , 可由式

)
对式( 3 ) 两边求导, 可得到lnZ 与lnsinh ( ασ p
的关系曲线( 见图 3 ), 对式( 3 ) 进行线性拟合, 可得 ( 6 ) 表示。
∂lnσ
15
到 A=5.8214×10 。 dJ ( 6 )
m = =
̇
dG ∂lnε ε , T
功率耗散因子 η 表示变形过程中显微组织变化
耗散量占总耗散量的比值, 一般 η 越大, 表明此区域
越稳定, 材料可加工性越好, 可由式( 7 ) 表示。
η
2m
η = ( 7 )
m +1
利用 Ori g in软件, 采用最小二乘法和三次样条
函数, 拟合出ln σ 与lnε之间的函数关系, 计算得到
̇
m , 再通过式( 7 ) 得到 。
η

) 的关系曲线 一般采用 ( ̇ )作为材料的失稳判据, 可由 式
图 3 lnZ 与lnsinh ( ασ p ξ ε
ξ ε <0 时, 表示材料处于失稳状态, 此
综上可得出 Q690 钢的热变形本构方程为 ( 8 ) 表示。 ( ̇ )
̇ 15 6.3963 时材料的加工性能较差, 易出现开裂、 偏析等缺陷,

ε= 5.8214×10 sinh0.012σ p
ξ ε >0 时,表示材料处于安

432.3545 不适合材料的加工;( ̇ )

ex p - RT ( 4 ) 全加工区域, 此时材料的加工性能较好。
2.3 热加工图的建立 m
∂ln
热加工图是评定材料可加工性能的重要依据, m +1
̇
ξ ε = +m <0 ( 8 )

̇
可用来选择变形工艺参数和改善材料的加工性能。 ∂ln ε
̇
研究 人 员 建 立 了 基 于 动 态 材 料 模 型 的 热 加 工 最后, 根据计算得出的结果, 将 η 绘制在 T-lnε
图 [ 7-15 ] , 认为材料变形所消耗的总功率 P 由塑性变 图中, 得到 Q690钢的功率耗散图, 将 ( ̇ ) <0的区域
ξ ε
2 4