Page 35 - 理化检验-物理分册 2021年第六期

薛 凯, 等: 试样原始横截面积计算方法对抗拉强度的影响

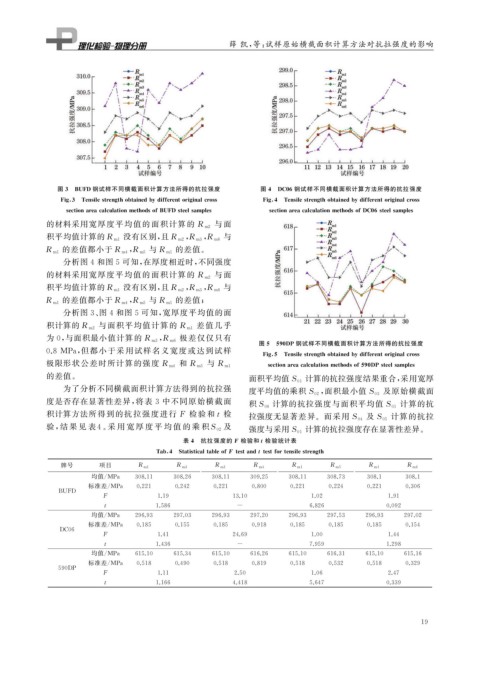
图 3 BUFD 钢试样不同横截面积计算方法所得的抗拉强度 图 4 DC06 钢试样不同横截面积计算方法所得的抗拉强度

Fi g 3 Tensilestren g thobtainedb ydifferentori g inalcross Fi g 4 Tensilestren g thobtainedb ydifferentori g inalcross

sectionareacalculationmethodsofBUFDsteelsam p les sectionareacalculationmethodsofDC06steelsam p les
与面
的材料采用宽厚度平均值的面积计算的 R m2
, , 与
积平均值计算的 R m1 没有区别, 且 R m2 R m3 R m6
, 的差值。
R m1 的差值都小于 R m4 R m5 与 R m1
分析图 4 和图 5 可知, 在厚度相近时, 不同强度
与面
的材料采用宽厚度平均值的面积计算的 R m2
, , 与
积平均值计算的 R m1 没有区别, 且 R m2 R m3 R m6
, 的差值;
R m1 的差值都小于 R m4 R m5 与 R m1
分析图 3 、 图 4 和图 5 可知, 宽厚度平均值的面
差值几乎
积计算的 R m2 与面积平均值计算的 R m1
, 极差仅仅只有
图 5 590DP 钢试样不同横截面积计算方法所得的抗拉强度
为0 , 与面积最小值计算的 R m3 R m6

0.8MPa , 但都小于采用试样名义宽度或达到试样
Fi g 5 Tensilestren g thobtainedb ydifferentori g inalcross

极限形状公差时所计算的强度 R m4 和 R m5 与 R m1 sectionareacalculationmethodsof590DPsteelsam p les
的差值。 计算的抗拉强度结果重合, 采用宽厚
面积平均值S 01
为了分析不同横截面积计算方法得到的抗拉强 及原始横截面
度平均值的乘积 S 02 , 面积最小值 S 03
度是否存在显著性差异, 将表 3 中不同原始横截面 计算的抗
积S 06 计算的抗拉强度与面积平均值 S 01
积计算方法所得到的抗拉强度进行 F 检验和 t 检
拉强度无显著差异。而采用 S 04 及 S 05 计算的抗拉
及
验, 结 果 见 表4 。 采 用 宽 厚 度 平 均 值 的 乘 积S 02 计算的抗拉强度存在显著性差异。
强度与采用S 01
表 4 抗拉强度的 F 检验和 t 检验统计表

Tab 4 Statisticaltableof Ftestandttestfortensilestren g th
牌号 项目 R m1 R m3 R m1 R m4 R m1 R m5 R m1 R m6

均值 / MPa 308.11 308.26 308.11 309.25 308.11 308.73 308.1 308.1
标准差 / MPa 0.221 0.242 0.221 0.800 0.221 0.224 0.221 0.306
BUFD
F 1.19 13.10 1.02 1.91

t 1.586 - 6.826 0.092
均值 / MPa 296.93 297.03 296.93 297.20 296.93 297.53 296.93 297.02
标准差 / MPa 0.185 0.155 0.185 0.918 0.185 0.185 0.185 0.154
DC06
F 1.41 24.69 1.00 1.44

t 1.436 - 7.959 1.298
均值 / MPa 615.10 615.34 615.10 616.26 615.10 616.31 615.10 615.16
标准差 / MPa 0.518 0.490 0.518 0.819 0.518 0.532 0.518 0.329
590DP
F 1.11 2.50 1.06 2.47

t 1.166 4.418 5.647 0.339

1 9