Page 63 - 理化检验-化学分册2017第八期

王 荣: 机械装备的失效分析( 续前)第 ６ 讲 X 射线分析技术

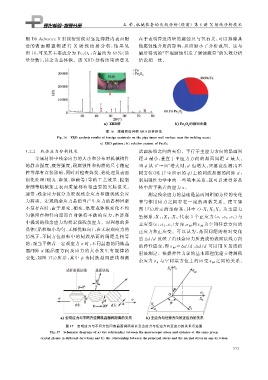
用 D８AdvanceX 射线衍射仪对靠近焊缝内表面附 在于表明管道内壁的腐蚀只与氧有关, 可以排除其
近的表 面 覆 盖 物 进 行 X 射 线 衍 射 分 析, 结 果 见 他腐蚀性介质的影响, 从而缩小了分析范围.这与
图 １６ , 可见其主要成分为 Fe ３O ４ 含量约为 ６９％ ( 质 最后得到的“ 空泡腐蚀引发了腐蚀疲劳” 的失效分析
,
量分数), 其余为基体铁.该 XRD 分析结果的意义 结论相一致.

图 １６ 焊缝附近异物 XRD 分析结果
Fi g 敭１６ XRDanal y sisresultsofforei g nmateiralsonthe p i p einnerwallsurfaceneartheweldin g seam
a XRDp attern b relativecontentofFe ３O ４
４．２．２ 残余应力分析技术 试面法线之间的夹角.平行于主应力方向的晶面间
金属材料中残余应力的大小和分布对机械构件 距d 最小, 垂直于主应力方向的晶面间距 d 最大.
的静态强度、 疲劳强度、 耐腐蚀性和构件的尺寸稳定 当 ψ 从 ０°→９０° 增大时, d 也增大, 只要设法测出不
性等都有直接影响, 同时对检查焊接、 热处理及表面 同方位( 图 １７ 中所示的 ψ ) 上的同族晶面的间距 d ,
强化处理( 喷丸、 渗氮、 渗碳等) 等的工艺效果、 控制 利用弹性力学中的一些基本关系, 就可以求得多晶
磨削等机械加工表面质量都有很重要的实际意义. 体中所平衡着的应力σ .
通常, 残余应力被分为宏观残余应力和微观残余应 测定残余应力的基础是晶面间距随方位的变化
力两类.宏观残余应力是指当产生应力的各种因素 率与作用应力之间存在一定的函数关系.建立如
不复存在时, 由于形变、 相变、 温度或体积变化不均 图 １７b ) 所示的坐标系, 其中 OＧX１X２X３ 为主应力
匀保留在构件内部而自身保持平衡的应力, 本讲座 坐标系, X１ X２ X３ 代表 ３ 个正应力( σ １ σ ２ σ ３ 与
, ,
, , )
中提到的残余应力均指宏观残余应力.对理想的多 为空间任意方向的
, , )
主应变( ε １ ε ２ ε ３ 方向, σ ϕψ 和 ε ϕψ
晶体( 晶粒细小均匀、 无择优取向), 在无宏观应力的 正应力和正应变.可以认为, 晶面间距的相对变化
情况下, 不同方位晶粒中的同族晶面的间距是相等
量 Δd / d 反映了由残余应力所造成的表面法线方向
的; 而当平衡着一宏观应力σ 时, 不同晶粒的同族晶
的弹性应变, 即ε ϕψ ＝Δd / d , Δd / d 可以用 X 射线衍
面间距d 随晶面方向及应力的大小发生有规律的
射法测定.根据弹性力学的基本原理能建立待测残
变化, 如图 １７a ) 所示, 其中 ψ 为同族晶面法线和测
余应力σ ϕ 与空间某方位上的应变ε ϕψ 之间的关系.

图 １７ 宏观应力与不同方位同族晶面间距离以及主应力与任意方向正应力的关系示意图
Fi g 敭１７ Schematicdia g ramsofa therelationshi pbetweenthemacrosco p icstressanddistanceofthesame g rou p
cr y stal p lanesindifferentdirectionsandb therelationshi pbetweenthe p rinci p alstressandthenormalstressinan ydirection

５ ７ １