Page 61 - 理化检验-物理分册2022年第十二期

程柄午, 等: 拉伸试验机的刚度修正

图 4 应变速率控制的力 - 时间曲线( 2 试验机)
#
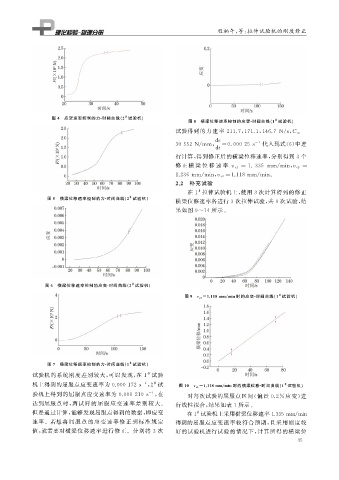
图 8 横梁位移速率控制的应变 - 时间曲线( 1 试验机)
#

试验得到的力速率 211.7 , 171.1 , 146.7 N / s , C m =
d e
30552N / mm , =0.00025s -1 代入到式( 6 ) 中进
dt
行计算, 得到修正后的横梁位移速率, 分别得到 3 个

修正 横 梁 位 移 速 率 v c1 =1.335 mm / min , v c2 =

1.236mm / min , v c3 = 1.118mm / min 。
2.2 补充试验
在1 拉伸试验机上, 使用 3 次计算得到的修正
#
图 5 横梁位移速率控制的力 - 时间曲线( 2 试验机)
#
横梁位移速率各进行 3 次拉伸试验, 共 9 次试验, 结
果如图 9~14 所示。

图 6 横梁位移速率控制的应变 - 时间曲线( 2 试验机)
#
图 9 v c3 =1.118mm / min时的应变 - 时间曲线( 1 试验机)

#

图 7 横梁位移速率控制的力 - 时间曲线( 1 试验机)
#
试验机的系统刚度差别较大, 可以发现, 在 1 试验
#

机上得到的屈服点应变速率为 0.000172s , 2 试 图 10 v c3 =1.118mm / min时的横梁位移 - 时间曲线( 1 试验机)
-1
#

#
验机上得到的屈服点应变速率为 0.000210s , 在 对每次试验的屈服点区间( 偏置 0.2% 应变) 进

-1
达到屈服点时, 两试样的屈服应 变速率差别较大。 行线性拟合, 结果如表 1 所示。
但是通过计算, 能够发现屈服点得到的数据, 即应变 #
在1 试验机上采用横梁位移速率1.335mm / min
速率。若想将屈服点的应变速率修正到标准 规定 得到的屈服点应变速率较符合预期, 且采用刚度较
值, 就需要对横梁位移速率进行修正。分别将 3 次 好的试验机进行试验的情况下, 计算所得的横梁位
4 5