Measurement uncertainty of dual extensometer and strain gauge coaxiality testers
-
摘要:
对双引伸计式和应变计式同轴度测试仪的测试原理进行分析,并对两种试验机的测量不确定度来源进行分析,研究了不同因素对两种试验机测量不确定度的影响程度。结果表明:采用双引伸计式同轴度测试仪时,应更关注引伸计的准确度、夹具对中情况,以及材料均匀性等因素;采用应变计式同轴度测试仪时,应额外考虑多截面贴片位置、数据采集系统线性误差,以及每次重新安装的定位偏差等因素;双引伸计式同轴度测试仪适用于常规的试验机同轴度日常检定;应变计式同轴度测试仪适用于精度要求高、分析全面的同轴度测试。
-
关键词:
- 双引伸计式同轴度测试仪 /
- 应变计式同轴度测试仪 /
- 校准装置 /
- 测量不确定度 /
- 弯曲百分数
Abstract:The testing principles of dual extensometer and strain gauge coaxiality testers were analyzed, and the sources of measurement uncertainty for the two testing machines were analyzed. The degree of influence of different factors on the measurement uncertainty of the two testing machines were study. The results show that when using a dual extensometer coaxiality tester, more attention should be paid to factors such as the accuracy of the extensometer, the alignment of the fixture and the uniformity of the material. When using a strain gauge coaxiality tester, additional factors such as the position of the multi section patch, linear errors in the data acquisition system, and positioning deviations during each reinstallation should be considered. The dual extensometer coaxiality tester was suitable for routine coaxiality calibration of testing machines. The strain gauge coaxiality tester was suitable for coaxiality testing that required high accuracy and comprehensive analysis.
-
同轴度是指在试验机施加力的过程中,试样夹持装置上下夹头中心线与试验机加载力轴线之间的同轴程度。在设计、加工、装配及日常使用等多个环节中,试验机均会产生几何误差和装配误差,因此不可避免地会存在同轴度误差。在对材料进行力学性能测试,尤其是拉伸试验时,一旦同轴度偏差过大,试样就会在承受轴向拉力的同时承受弯曲、偏心等附加力,从而使测试结果的准确性与重复性受到影响。目前,常见的试验机同轴度测试装置主要有:双引伸计式同轴度测试仪和应变计式同轴度测试仪。前者通过测试标准棒在特定长度段内的平均弯曲变形来计算试验机的同轴度(通常以弯曲百分数表示),后者通过测试标准棒在多个截面上的弯曲应变,并对其应变进行计算,从而获得同轴度。在测试过程中,测试结果的准确性和溯源性极为关键,对测试过程中各类不确定度源进行评定与合成是确保测试质量的重要环节。
1. 同轴度测试仪的测试原理和测试结果
1.1 双引伸计式同轴度测试仪
双引伸计式同轴度测试仪通常由一根具有已知精度和材料特性的标准试棒、两对对称布置的高精度引伸计、数据采集系统,以及安装夹具等部分组成(见图1)。
1.1.1 标准试棒与测试段
标准试棒的材料一般为优质合金钢或其他弹性稳定性良好的材料,利用高精度车削、热处理和标定加工等方式来保证试棒的圆度、直线度等指标满足相关要求。在试棒的中部或两端预先设置测试段,便于引伸计的夹持定位和读数[1]。
1.1.2 引伸计的安装与对称测试
将两只引伸计(或两对)对称地安装在试棒圆周面上,呈上下或左右成对分布,以便试棒在加载过程中进行轴向变形与弯曲变形。当试验机对标准试棒施加纯拉力且同轴度良好时,试棒的横截面不会产生明显的弯曲变形;若同轴度偏差明显,则试棒会产生偏心力矩,导致两侧引伸计记录的应变存在差异。
1.1.3 弯曲百分数的计算
双引伸计式同轴度测试仪一般通过比较成对引伸计的变形来获得弯曲变形量,并将其与平均轴向变形进行比对,进而求得弯曲百分数。在测试过程中,需要逐步增大拉力至若干预定载荷点,分别测得该载荷下的弯曲百分数,然后确定试验机的同轴度是否符合JJG 139—2014 《拉力、压力和万能试验机》的要求。
这种测试方法的优点是操作相对直观,可直接读取引伸计示值,便于进行对称差异的比较与记录;缺点是装置结构相对复杂,对引伸计安装的同心度与夹具的精确度要求较高,一旦安装偏差过大,测试结果就会产生附加影响。此外,在使用过程中还需定期对引伸计进行校准与溯源,以确保其量程和灵敏度符合测试精度的要求。
双引伸计式同轴度测试仪在我国现行标准(如JJG 139—2014、JJG 475—2008 《电子式万能试验机》等)中应用广泛,适用于常规拉力、压力和万能试验机的日常检定与校准;而在美国材料与试验协会(ASTM)颁布的 ASTM E1012-14e1 Standard Practice for Verification of Testing Frame and Specimen Alignment under Tensile and Compressive Axial Force Application中,更加强调通过应变计装置来评估加载系统与试样的对中性,因此对于高精度或质量较大的试验机,更倾向采用应变计式同轴度测试仪。
1.2 应变计式同轴度测试仪
应变计式同轴度测试仪的外观如图2所示,该装置通常选用一根经过应变花或应变片布置和标定的标准试棒,通过测试标准试棒不同截面上的弯曲应变与轴向应变来计算同轴度。
1.2.1 标准试棒及应变片布置
标准试棒的材料为高强度、高弹性合金钢。在标准试棒预先确定的若干个截面上黏贴应变片或应变花。每个截面至少设置3片应变片,围绕试棒周向呈90°或120°间隔分布,以确保能同时测试到各方位的应变。
1.2.2 测试过程与数据获取
在测试过程中,试验机向标准试棒施加轴向拉力。如果试验机的同轴度良好,则各应变片测得的轴向应变基本相同,而弯曲应变接近于零或在某个较小范围内波动;如果存在显著的偏心或弯曲力矩,则各截面应变会出现明显的差异。通过对各截面应变的加权平均或差值运算,即可推算出标准试棒的实际弯曲应变。
1.2.3 弯曲应变与弯曲百分数
应变计式同轴度测试仪各个截面应变差值与平均应变的比为弯曲应变百分数。当载荷逐渐增大时,记录各加载点对应的弯曲应变百分数曲线。如果该数值始终保持在标准允许的范围内,就说明试验机的加载轴线与试样中心线的同轴度良好;若偏差超过标准要求,则须调整夹具或修正其他装配[2]。
应变计式同轴度测试仪能够在多个截面上同步测试试棒的同轴度,能更全面地反映不同载荷下试棒的弯曲应变变化情况。但应变计式同轴度测试仪的操作更为复杂,需要在试棒制作阶段就完成应变片的黏贴与标定,而且要保证应变片的黏贴质量与周向分布的均匀性,否则易引入额外的测试误差。数据采集系统也需具备足够的通道数和采集精度,才能有效同步记录多路应变。
应变计式法在标准ASTM E1012-14e1中的应用更为常见,尤其是对于对中性要求高的拉-压试验,使用该方法可准确地判断试验机加载力轴线与试样中心线的重合程度。
1.3 同轴度的测试结果
无论采用双引伸计式还是应变计式同轴度测试仪,核心指标均为弯曲百分数e,其计算方法如式(1)所示。
(1) 式中:ΔLmax为最大弯曲变形量;
为平均轴向变形量。 记录不同载荷点下的ΔLmax与
,若e在某一限值以内,则可判定该试验机在该载荷段下的同轴度满足要求。 采用应变计式同轴度测试仪时,在多个截面布置应变片,记录各应变片与平均应变的差值,则弯曲百分数e的计算方法如式(2)所示。
(2) 式中:εi为第i个应变片的应变;εavg为该截面应变片的平均应变;n为应变片数量。
2. 测量不确定度的来源
2.1 传感器和数据采集系统不确定度
引伸计或应变计的灵敏度、线性度、迟滞、重复性及零点漂移等因素,均会导致读数出现偏差或波动。此外,数据采集仪表的分辨力和线性度也会对测量不确定度产生影响。
2.2 试棒尺寸和材料特性不确定度
标准试棒的外径、圆度、弹性模量等都存在制造和标定误差。尤其当采用应变计式同轴度测试仪时,需要对应变片黏贴位置的实际周向角度进行精确度评估;当采用双引伸计式同轴度测试仪时,试棒的加工精度与长度段定位也存在一定误差。
2.3 夹具和试验机本身的安装误差
试验机夹头装配不当或紧固力不均匀会使标准试棒初始位置偏心或倾斜,从而导致试验机在低载荷下就产生不对称的应变分布。此外,在施加力的过程中,试验机横梁或立柱可能存在微小变形或松动,也会带来额外的同轴度误差[3]。
2.4 环境条件和操作误差
温度、湿度、振动等环境因素会影响引伸计或应变计的稳定性,试棒也会因温度变化而产生热膨胀或材料性能漂移。操作人员在安装、对中及读数时可能存在主观判断偏差或反应迟滞。
根据以上不确定度源,可建立测量方程,运用A类评定和B类评定相结合的方法来评估各不确定度分量。首先,通过多次重复试验获取随机误差(A类评定),然后结合传感器检定证书、标准试棒标定证书等文献或历史数据(B类评定),逐项给出不确定度分量的方差或标准不确定度。
3. 双引伸计式同轴度测试仪不确定度分量评定
双引伸计式同轴度测试仪测量结果的不确定度分量统计结果如表1所示(表中:xi max为3次测量值中的最大值;xi min为3次测量值中的最小值;L为轴向变形;r为同轴度传感器的分辨力;R为铝棒材料的均匀性;St为铝棒温度系数;Δt为试验前、后实验室温度和机器温度的相对变化),双引伸计式同轴度测试仪在相互垂直方向上各测试一次会有前、后、左、右4个数据。
Table 1. 双引伸计式同轴度测试仪测量结果的不确定度分量统计结果不确定度来源 评定类型 分布情况 不确定度u/% 同轴度测试仪测量结果的复现性引入的不确定度 A — 
试验机力值控制误差引入的不确定度 B 均匀 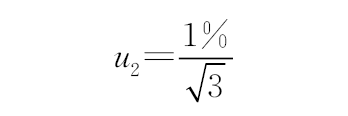
引伸计准确度引入的不确定度 B 均匀 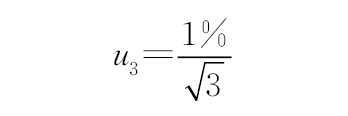
同轴度测试仪分辨力引入的不确定度 B 均匀 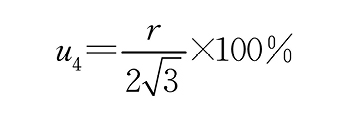
铝棒材料均匀性引入的不确定度 B 均匀 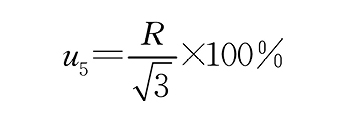
铝棒温度变化引入的不确定度 B 反正弦 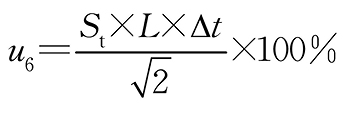
拉伸时打滑因素引入的不确定度 B 均匀 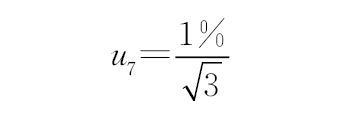
在试验机力值传感器最大使用范围的4%,6%,8%条件下,对各不确定度分量进行评定。
3.1 载荷为4%时同轴度的不确定度评定
3.1.1 同轴度测试仪测量结果的复现性引入的不确定度
,同理u12=5.84×10-4 mm,u13=1.25×10-3 mm,u14=5.06×10-4 mm,其中u11,u12,u13,u14分别为u1前、后、左、右4个数据对应的不确定度分量。 3.1.2 试验机力值控制误差引入的不确定度
试验机精度为0.5级,应力控制误差为±1%,分布均匀,由于前、后、左、右4个数据对应的ΔLi(引伸计3次测量值的平均值)分别为:ΔL1=0.026 72 mm,ΔL2=0.027 54 mm,ΔL3=0.025 23 mm,ΔL4=0.024 19 mm,因此
,同理u22=1.59×10-4 mm,u23=1.46×10-4 mm,u24=1.40×10-4 mm,其中u21,u22,u23,u24分别为u2前、后、左、右4个数据对应的不确定度分量。 3.1.3 引伸计准确度引入的不确定度
引伸计精度为1级,分布均匀,由于ΔL1=0.026 72 mm,ΔL2=0.027 54 mm,ΔL3=0.025 23 mm,ΔL4=0.024 19 mm,因此
,同理u32=1.59×10-4 mm,u33=1.46×10-4 mm,u34=1.40×10-4 mm,其中u31,u32,u33,u34分别为u3前、后、左、右4个数据对应的不确定度分量。 3.1.4 同轴度测试仪分辨力引入的不确定度
同轴度测试仪引伸计分辨力为0.000 01 mm,均匀分布。因此
,其中u41,u42,u43,u44分别为u4前、后、左、右4个数据对应的不确定分量。 3.1.5 铝棒材料均匀性引入的不确定度
铝棒变形为弹性阶段,弹性范围内材料的不均匀性对其力学性能的影响非常小,因此,铝棒材料均匀性对测量结果不确定度的影响可以忽略。
3.1.6 铝棒温度变化引入的不确定度
铝合金的热膨胀系数为2.3×10−5 ℃−1,引伸计夹持距离为100 mm,现场温度变化允许值为2 ℃,半区间为1 ℃,反正弦分布,因此温度变化引入的不确定度
,其中u61,u62,u63,u64分别为u6前、后、左、右4个数据对应的不确定度分量。 3.1.7 拉伸时打滑等因素引入的不确定度
根据多次试验结果,分析出拉伸时打滑等因素引入的不确定度
,同理u72=1.59×10-4 mm,u73=1.46×10-4 mm,u74=1.40×10-4 mm,其中u71,u72,u73,u4分别为u7前、后、左、右4个数据对应的不确定度分量。 3.1.8 合成不确定度
0.002 094 mm,同理 , 0.002 065 mm, ,其中 , , , 分别为前、后、左、右4个数据对应的合成不确定度。 3.1.9 同轴度测试仪测量结果的不确定度ue
经计算
, 5.649mm-1, , -6.103mm-1,其中c1,c2,c3,c4分别为前、后、左、右4个数据对应的灵敏系数,因此 ×100%=1.63%。 3.1.10 测量结果的扩展不确定度
测量结果的扩展不确定度
,其中包含因子k=2。 3.2 载荷为6%时同轴度的不确定度评定
3.2.1 同轴度测试仪测量结果的不确定度ue
经计算
, 3.740mm-1, , -3.646mm,因此 ×100%=1.02%。 3.2.2 测量结果的扩展不确定度
测量结果的扩展不确定度
,其中包含因子k=2。 3.3 载荷为8%时同轴度的不确定度评定
3.3.1 同轴度测试仪测量结果的不确定度ue
, , , ,因此 ×100%=0.76%。 3.3.2 测量结果的扩展不确定度
测量结果的扩展不确定度UC=k×ue=1.5%,其中包含因子k=2。
4. 应变计式同轴度测试仪不确定度分量评定
应变计式同轴度测试仪测量结果的不确定度分量统计结果如表2所示(表中
为3次测量值的平均值)。 Table 2. 应变计式同轴度测试仪测量结果的不确定度分量统计结果不确定度来源 评定类型 分布情况 不确定度u/% 同轴度测试仪测量结果的复现性引入的不确定度 A — 
试验机力值控制误差引入的不确定度 B 均匀 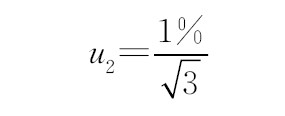
数据采集系统引入的不确定度 B 均匀 
同轴度测试仪分辨力引入的不确定度 B 均匀 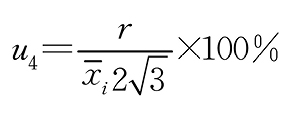
同轴度测试仪线性误差引入的不确定度 B 均匀 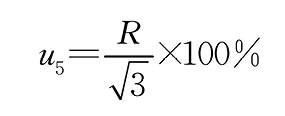
温度变化引入的不确定度 B 均匀 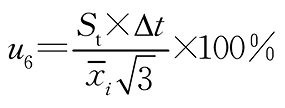
安装位置、间隙误差和定心程度等因素引入的不确定度 B 均匀 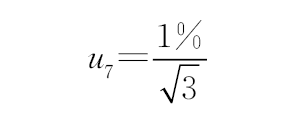
在试验机力值传感器最大使用范围的4%,6%,8%条件下,对各不确定度分量进行评定,结果如表3所示。
Table 3. 应变计式同轴度测试仪测量不确定度评定结果试验机力值传感器最大使用范围的倍数 扩展不确定度UC/% 0.04 3.1 0.06 1.4 0.08 2.2 5. 综合分析
在实际使用中,许多机构在对同一台试验机进行同轴度测试时,会分别使用双引伸计式和应变计式同轴度测试仪,以对比测试结果的一致性。若测试结果在允许偏差范围内具有较好的一致性,说明两种试验机都能准确反映其同轴度水平;若二者差异较大,则需分析其不确定度构成是否存在明显不同,或者试验机本身存在超差或校准过期等问题[4]。
通常情况下,应变计式同轴度测试仪可测量多截面、多应变片的数据,对不对中应力的空间分布掌握更全面,能更敏感地捕捉到局部弯曲效应,从而在某些载荷点呈现相对更大的弯曲百分数。若需要进行更精确、更全面的同轴度测试,则应选择应变计式同轴度测试仪;若需进行日常快速测试或判断同轴度是否大幅偏离标准,则应选择双引伸计式同轴度测试仪。
在各类设备的比对试验中,还应关注随机误差对重复性与再现性的影响。通过多次重复测试试样,可得到弯曲百分数随加载力的变化曲线,以及用统计方法量化的重复性。这一过程不仅有助于判断装置本身的性能,也可反映试验机的夹具及加载力系统是否存在不稳定或非线性问题,从而为后续优化试验流程、改进设备结构提供指导。
6. 结语与建议
双引伸计式与应变计式同轴度测试仪的弯曲应变测量范围和数据处理方法不同。采用双引伸计式同轴度测试仪时,应更关注引伸计的准确度、夹具对中情况,以及材料均匀性等因素;采用应变计式同轴度测试仪时,应额外考虑多截面贴片位置、数据采集系统线性误差,以及每次重新安装的定位偏差等因素。
双引伸计式同轴度测试仪的结构相对简单,可直接读取数据,适合常规的试验机同轴度日常检定;应变计式装置布置较为复杂,但能在多个截面同步监测弯曲应变,适合精度要求高或需要较全面分析同轴度分布的场合。引伸计、应变计和数据采集系统在长期使用中易受到冲击、疲劳、温度变化等因素的影响,导致零点漂移或灵敏度波动;标准试棒也可能在频繁装夹或弯曲应力作用下发生微小变形或性能退化。因此,建议使用单位建立周期性校准和维护制度,按照标准要求对测量装置进行溯源和验证,确保其量值准确度符合规定。
在条件允许的情况下,建议检测机构或使用单位开展双引伸计式和应变计式同轴度测试仪之间的比对试验,一方面可对两种试验机的测量结果进行交叉验证,检验其一致性与重复性;另一方面,通过收集、分析这些比对数据,还能进一步完善不确定度评定模型,明确在各种典型载荷水平下的弯曲应力分布规律,从而提高对试验机同轴度的综合评判能力。
双引伸计式与应变计式同轴度测试仪在测量原理、设备结构和适用范围上各有优势,但无论采用何种测量方式,只有结合系统化的不确定度分析方法,才能最大限度地保障测试数据的准确性与可靠性。未来可在传感器精度提升、数字化监测手段应用以及测量模型的进一步完善等方面继续深化研究,为材料力学性能测试提供更稳定、更可溯源的技术支持。
-
Table 1 双引伸计式同轴度测试仪测量结果的不确定度分量统计结果
不确定度来源 评定类型 分布情况 不确定度u/% 同轴度测试仪测量结果的复现性引入的不确定度 A — 
试验机力值控制误差引入的不确定度 B 均匀 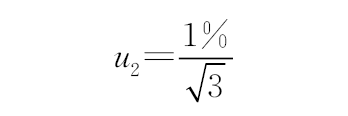
引伸计准确度引入的不确定度 B 均匀 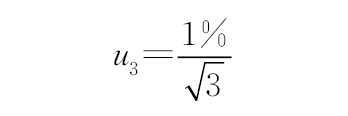
同轴度测试仪分辨力引入的不确定度 B 均匀 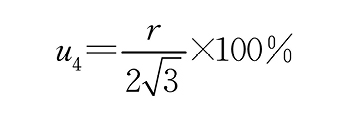
铝棒材料均匀性引入的不确定度 B 均匀 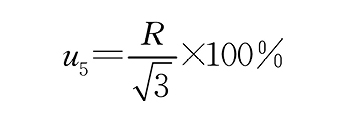
铝棒温度变化引入的不确定度 B 反正弦 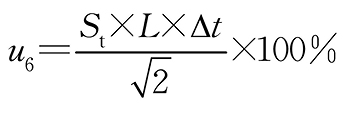
拉伸时打滑因素引入的不确定度 B 均匀 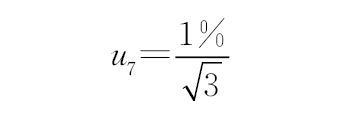
Table 2 应变计式同轴度测试仪测量结果的不确定度分量统计结果
不确定度来源 评定类型 分布情况 不确定度u/% 同轴度测试仪测量结果的复现性引入的不确定度 A — 
试验机力值控制误差引入的不确定度 B 均匀 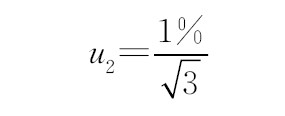
数据采集系统引入的不确定度 B 均匀 
同轴度测试仪分辨力引入的不确定度 B 均匀 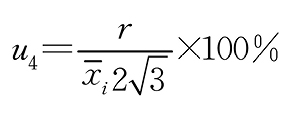
同轴度测试仪线性误差引入的不确定度 B 均匀 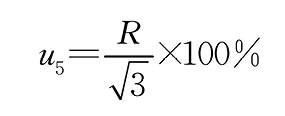
温度变化引入的不确定度 B 均匀 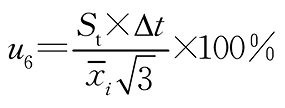
安装位置、间隙误差和定心程度等因素引入的不确定度 B 均匀 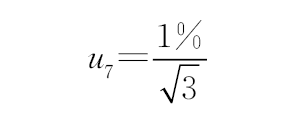
Table 3 应变计式同轴度测试仪测量不确定度评定结果
试验机力值传感器最大使用范围的倍数 扩展不确定度UC/% 0.04 3.1 0.06 1.4 0.08 2.2 -
[1] 胡志刚,曾琼,张亚麟,等 .基于经纬仪检定仪的激光垂准仪校准装置的研制[J].江西科学,2023,41(6):1136-1140. [2] 王斌,胡国林,郭钊 .试验机同轴度对金属材料弹性模量测量的影响[J].理化检验(物理分册),2021,57(4):12-14. [3] 王宏业基于多偏置误差分离的航空发动机低压涡轮轴同轴度测量方法哈尔滨哈尔滨工业大学2020王宏业 .基于多偏置误差分离的航空发动机低压涡轮轴同轴度测量方法[D].哈尔滨:哈尔滨工业大学,2020. [4] 秦海峰,王晶露,刘思博,等 .材料试验机同轴度检测方法及影响因素分析[J].测控技术,2020,39(3):65-70.




 下载:
下载:

